AUSTRALIAN CURRICULUM ALIGNMENT: 

• Movement of materials across membranes occurs via diffusion, osmosis, active transport and/or endocytosis

BACKGROUND: 

The relatively small size of cells allows molecules in and out of their membranes. If a cell gets too large then the centre cannot be serviced efficiently. As the size of an object increases, the volume increases at a greater rate than surface area. For a cell, this means that efficiency of the exchange of materials across a membrane is reduced, and therefore the cell’s ability to take in enough nutrients is reduced. Furthermore, toxins may be retained for too long. Using Agar Cubes with indicator, vinegar and some simple mathematics, we can see how much effect a small increase in surface area has on volume.

In this practical, students are given Agar Cubes of three different sizes, impregnated with indicator to display an alkaline pH. Initial measurements make it clear that the surface-area-to-volume ratio is large for small cubes, with the ratio reducing as cube size increases. The cubes are placed in vinegar, and as the acid diffuses into the cell to reduce the pH and change the colour of the indicator, students see that a small difference in size can make a large difference to the time it takes to completely penetrate to the centre. Students also have the opportunity to calculate the results and plot graphs. Alternatively, a spreadsheet with the equations programmed in can be used.

PREPARATION - BY LAB TECHNICIAN

• To make 0.1M NaOH, add 0.4 g of NaOH pellets to 100 mL of distilled water. Stir constantly to dissolve.
• To make 0.1% bromothymol blue, add 0.1 g of bromothymol blue powder to 1.6 mL of 0.1M NaOH. Stir constantly to dissolve. Add boiling water to make a 100 mL solution. Stir to combine.
• To make agar, add 18 g of plain agar powder to 570 mL of distilled water. Stir to suspend powder. Boil and stir constantly until fully dissolved. Add 30 mL of the 0.1% bromothymol blue solution. Stir to combine. Add 1 mL of NaOH to achieve a deep blue colour. Add more NaOH if agar remains slightly green.
• To form agar cubes, pour into ice cube moulds of the appropriate sizes (3cm, 2cm and 1cm). Refrigerate to set. Remove cubes from the trays once the agar is fully set.

NOTE: It is best to leave the the cubes in sealed packaging in the fridge until ready for use.

METHOD - STUDENT ACTIVITY

1.  Form a hypothesis for this investigation. Remember that you must record all aspects of this investigation into your logbook.
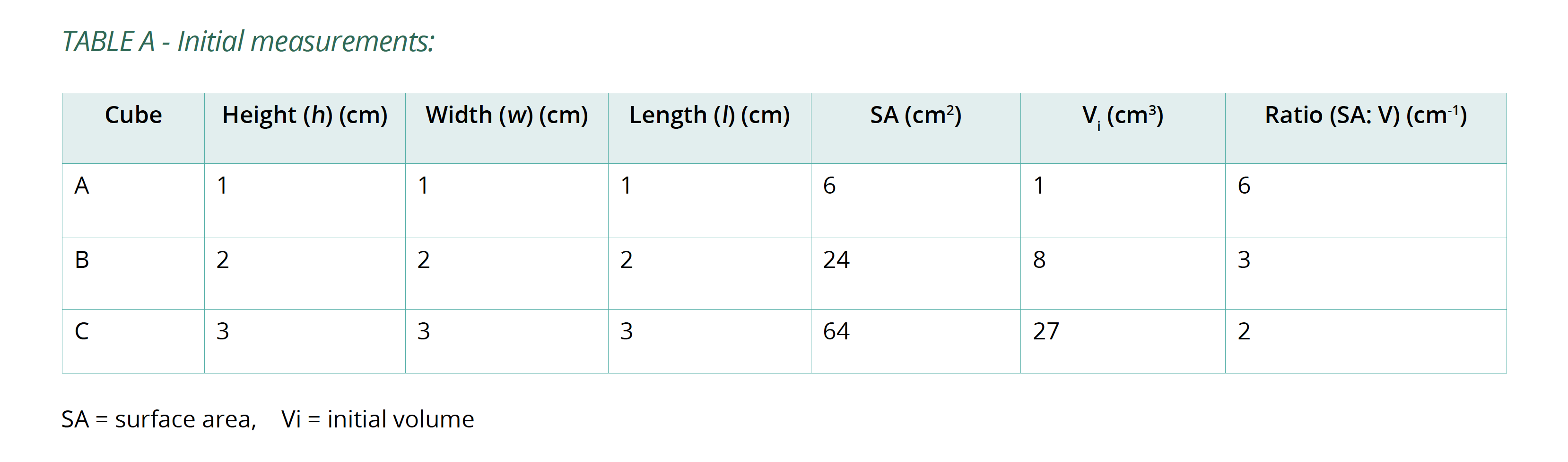
2. Put on disposable gloves and measure the height (h), width (w) and length (l) of each cube to calculate surface area (SA) and initial volume (Vi). Copy Table A into your logbook and record this information in it.
3. Half-fill the beaker with vinegar, ensuring that the largest cube can be submerged, and place one cube of each size into the beaker.
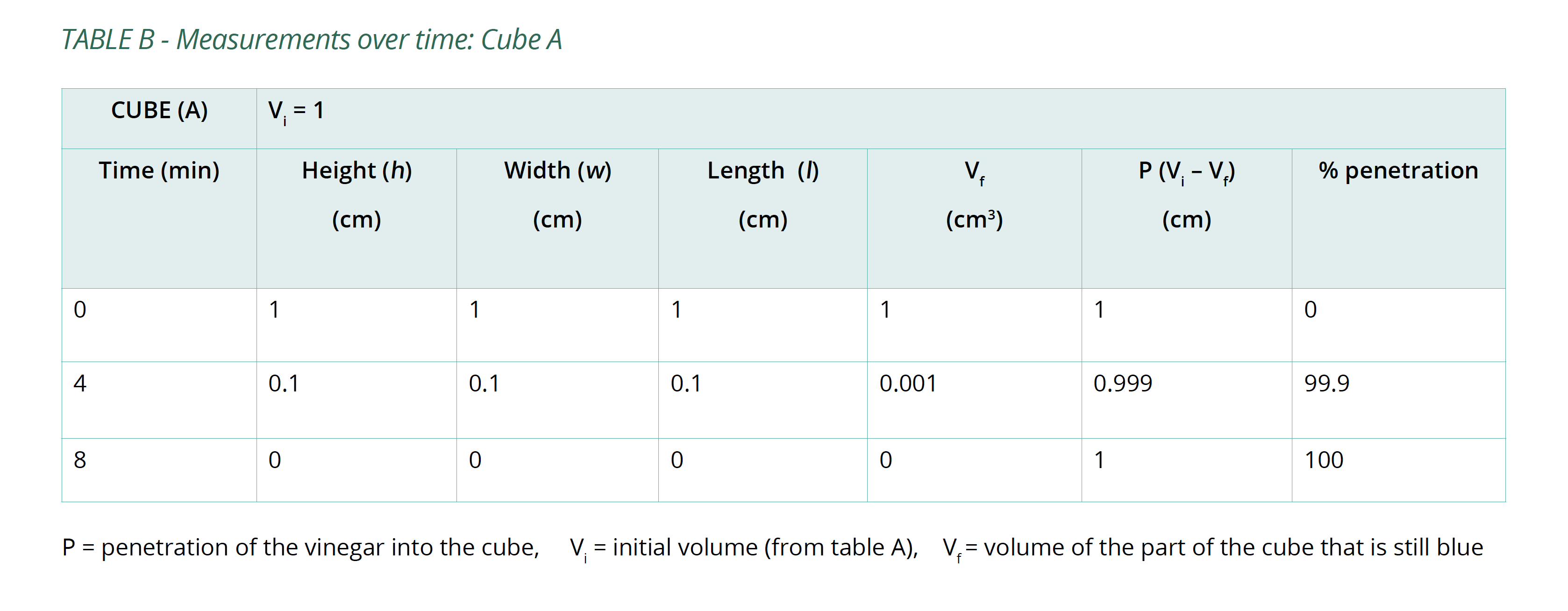
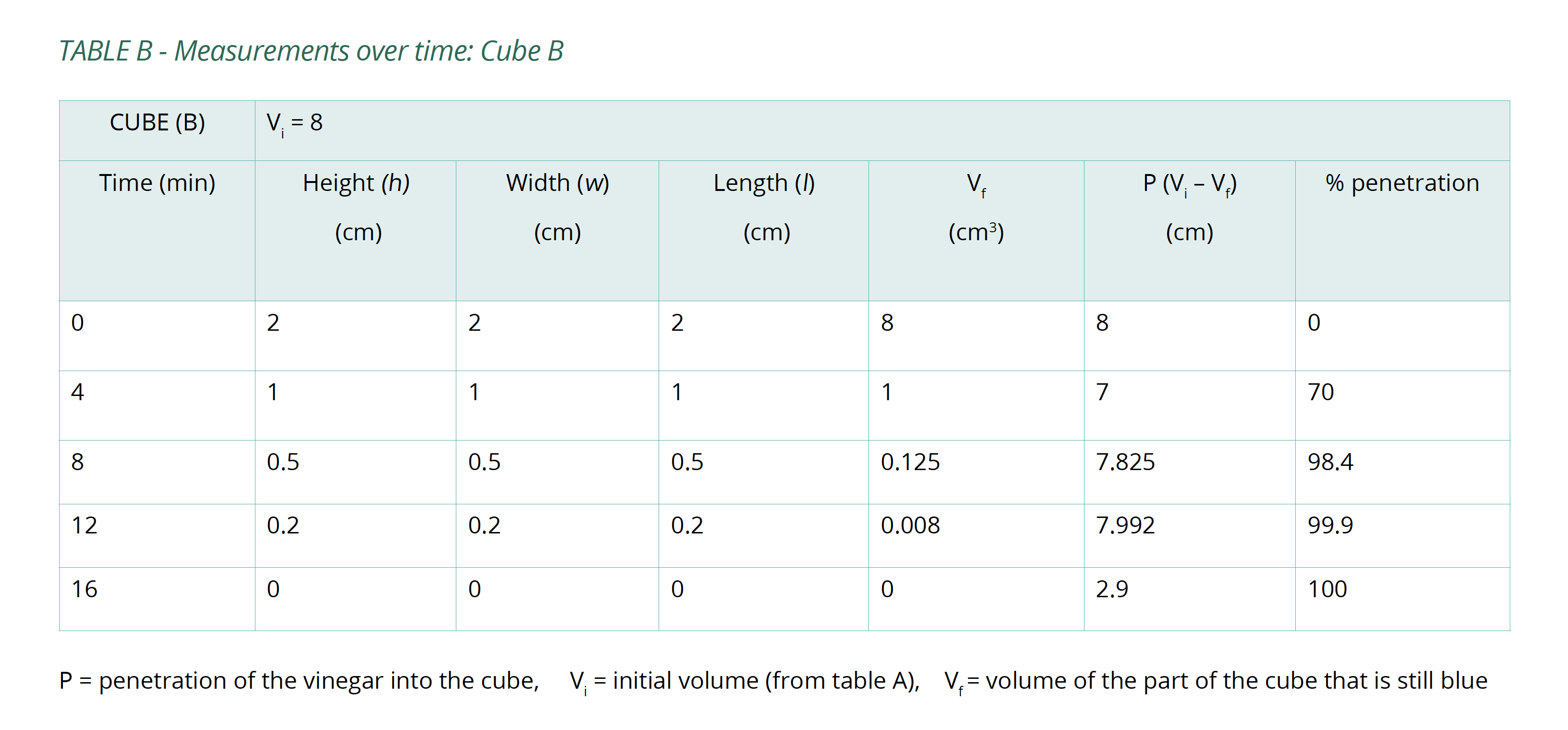
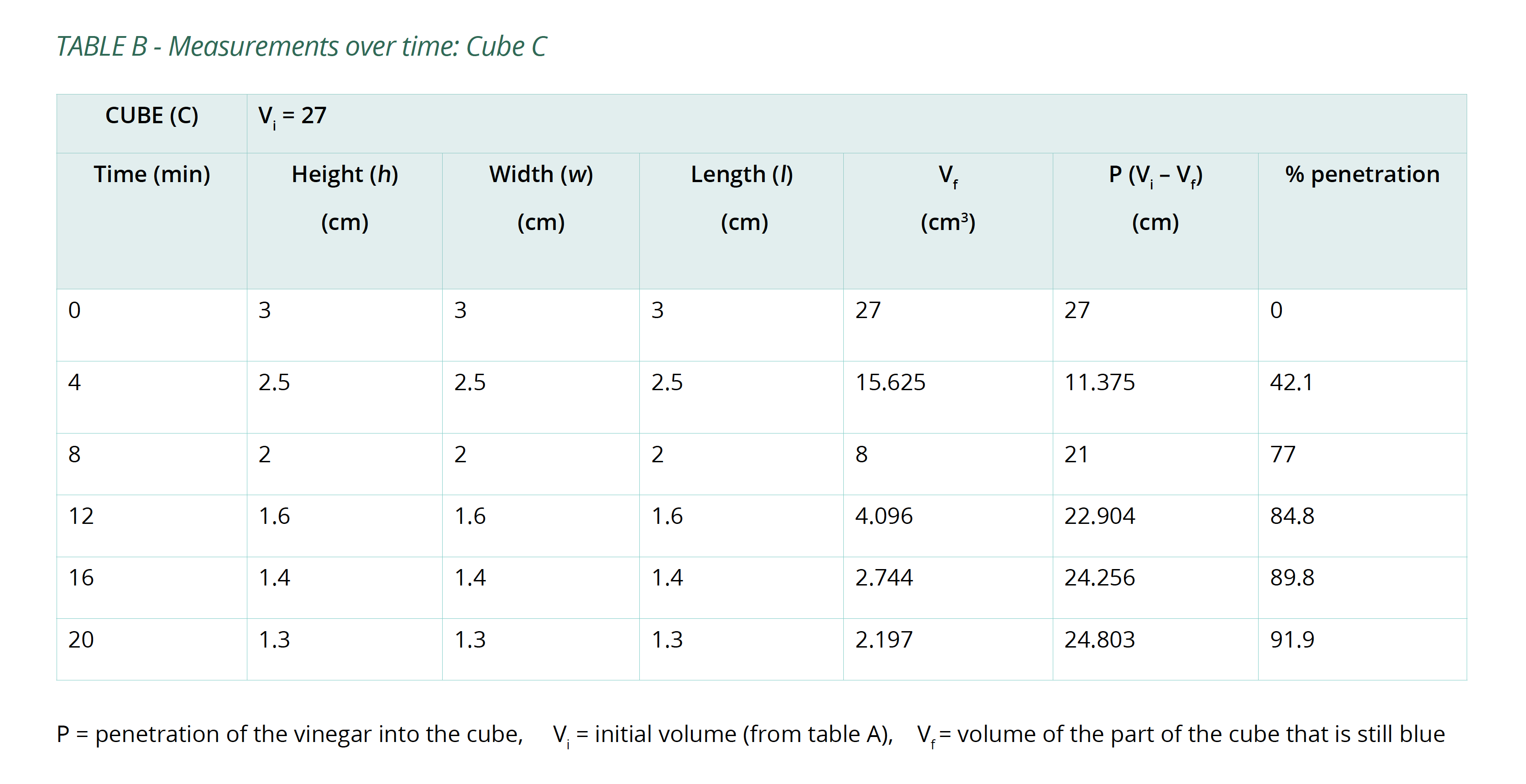
4. Set a timer and remove the cubes after 4 minutes, pat them dry with a paper towel. Measure the portion of each cube that is still blue. Try to minimise the amount of time the cubes are out of the vinegar.
5. Replace the cubes in the vinegar and repeat step 4 several times until the cubes have been submerged for a total of 20 minutes.
6. Calculate the volume of the portion of the cube that is still blue (Vf) after each 4-minute interval and the percentage of the whole cube that the vinegar has penetrated (%P). Copy Table B into your logbook and record this information in it.

OBSERVATION AND RESULTS

Below is an example of the results tables from this experiment. Students will complete Table A with the initial measurements, and then continue to fill in Table B with their measurements as the results of their experiment in Table B. The calculations of surface area and volume show that the surface area of the largest cube is close to six times that of the smallest, while the volume has increased to about fourteen times that of the smallest. As well, the time taken for the cubes to lose colour has increased beyond what may be expected for the change in size.

INVESTIGATION

• Explain why the agar cubes change colour when placed in the vinegar solution. 
• The cubes are impregnated with a pH indicator, and start off alkaline. As the vinegar diffuses through the cube, the indicator changes colour to denote the lowered pH. 
• Describe the relationship between the size and surface area to the rate that diffusion occurs. 
• As an object increases in size, the volume of the object increases more in proportion to the increase in surface area (assuming the increase is in three dimensions). As diffusion is limited by the surface area it can access, it will take longer to reach the centre of a large object than that of a small object.  
• Ask the students to think about the way the numbers are calculated. Students may recognise that surface area is two numbers multiplied by each other, while volume is three numbers multiplied by each other. For example, 2x2=4 and 2x2x2=8, while 3x3=9 and 3x3x3=27. Although the surface area of one face is multiplied by six to get the total surface area of the cube, this number remains the same and does not increase as the cube increases. Note: multiplying by six works for a perfect cube. For an imperfect cube, the surface area of each face is calculated and then each is added together, but the concept remains the same.
• Using the same set of axes, create a graph of time in minutes (x-axis) against %P (y-axis) for each cube. Comparing them all on one graph will demonstrate the trends of each. 

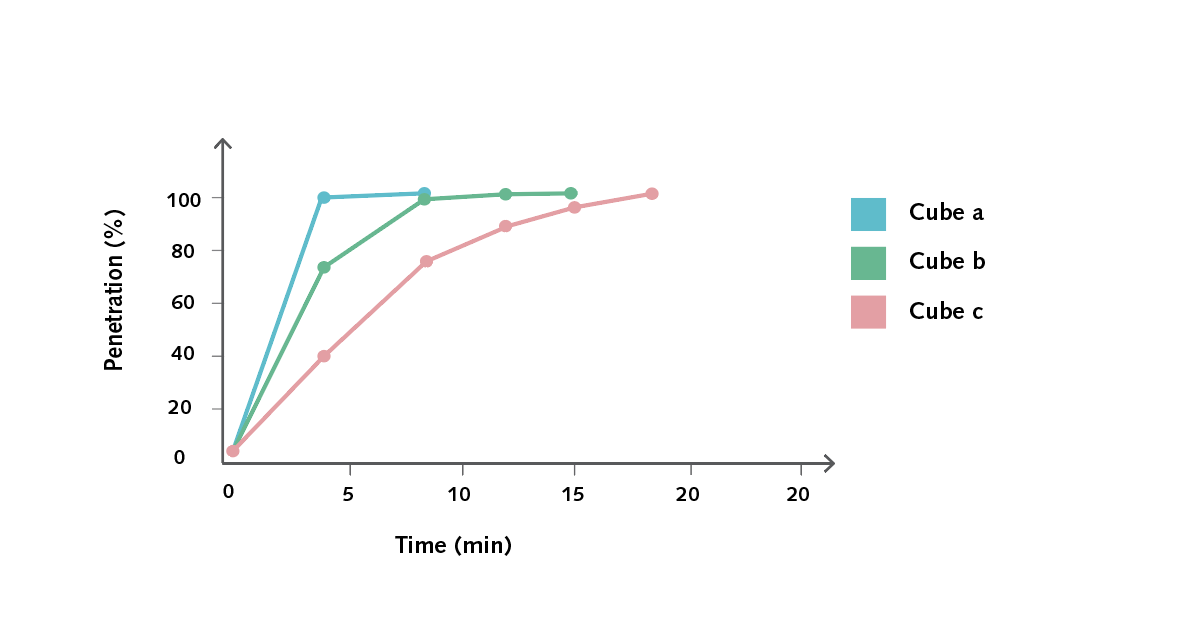
• Summarise your findings, commenting on your hypothesis and explaining the advantages and disadvantages of cell size.

• Create a graph of initial SA : V (x-axis) against the total time in minutes (y-axis) to demonstrate that, as the ratio increases, the time taken to completely penetrate the cube will decrease in a non-linear fashion.

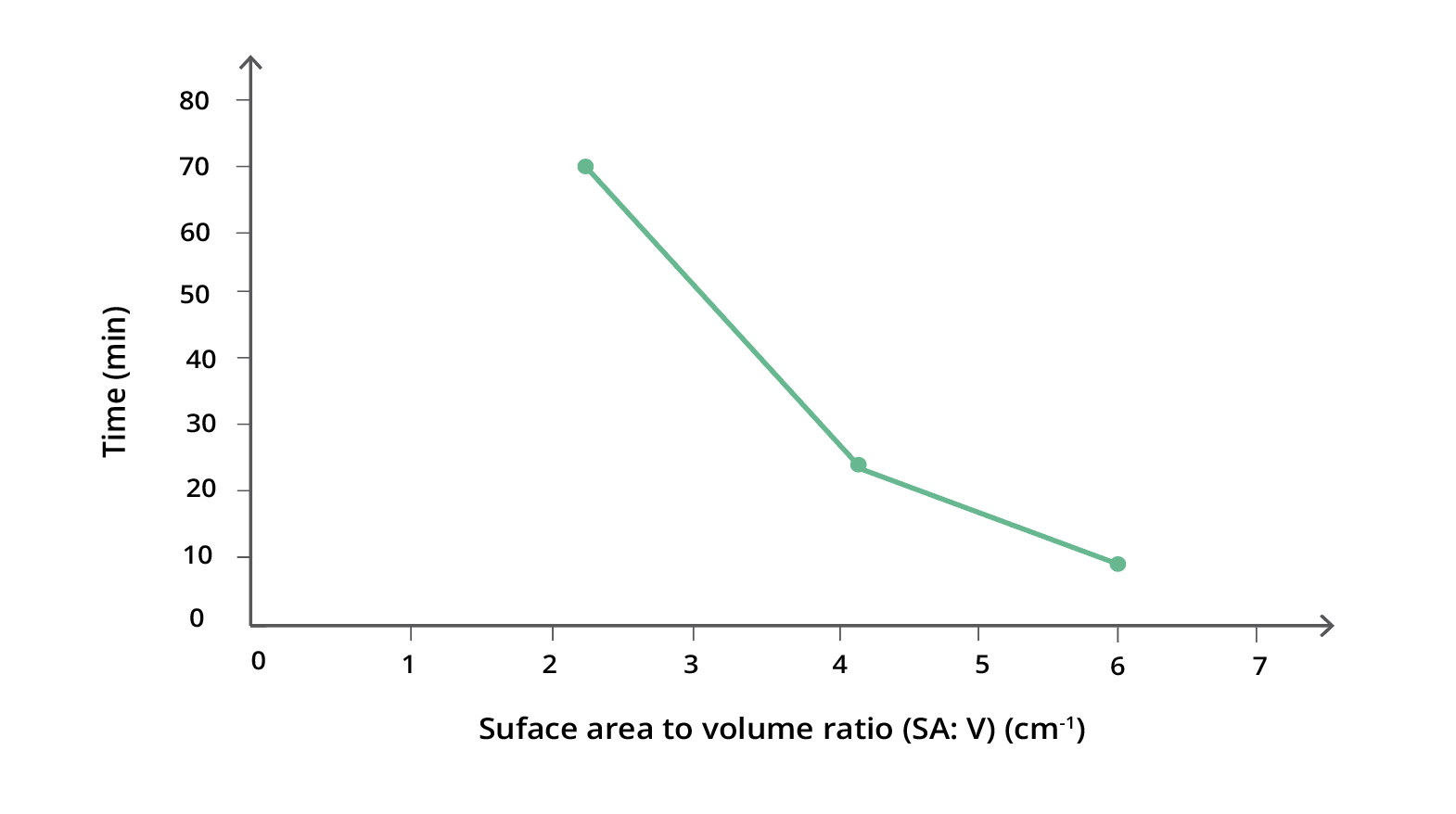
TEACHER TIPS: 

• If Agar Cubes have turn green prior to the experiment, place them in a beaker containing a 5% bromothymol blue solution, and add sodium hydroxide using a plastic pipette until the cubes return to blue. Be aware this process may take a few hours.